Today topic is about trigonometry. I am going to review cahpter 4.1. This chapter is about radian measure. I am going to tell you how we can measure the redian and degree. The main question you would have is that what is radian?
Radian is the ratio between the length of an arc and its radius.The radian is the standard unit of angular measure, used in many areas of math. Here is a picture that you can understand better. Arc lentgh divided by radius is one radian.
Now that we know what is radian, we are going to know how we can measure it. The frist obtion is that if we have degree how we can measure it to radian? The formula is that if we degree measure and we want to measure it to radian we should use this formula:
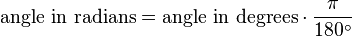
On the other hand if we have radian, and we want to measure degree we should use this formula:

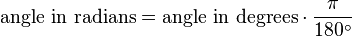



Very knowledgeable blog.There are an enormous number of uses of trigonometry and trigonometric functions. For instance, the technique of triangulation is used in astronomy to measure the distance to nearby stars, in geography to measure distances between landmarks, and in satellite navigation systems. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.
ReplyDeleteICSE Geography Syllabus